Division of Chemical Nomenclature and Structure Representation
H. A. Favre, P. M. Giles Jr, K.-H. Hellwich, A. D. McNaught, G. P. Moss, W. H. Powell
Since publication of "Revised Section F: Natural Products and Related Compounds" in Pure Appl. Chem. 71 (1999) 587-643 a number of errors have been detected. Further consideration of some sections now requires some extensions or further explanation. These changes and corrections were published in Pure Appl. Chem. 76 (2004) 1283-1292 and are available in PDF format.
The published version has examples collected into schemes which have not been used in the web version. To assisted correction of the printed version the scheme numbers are shown below.
Introduction iii. (b) Change "heteroatoms and groups" to "heteroatoms and characteristic groups".
RF-1.4 Note. Correct reference to R-2.3.3.1.
RF-1.6 second sentence. Twice change "groups" to "characteristic groups".
RF-3.2.1. Change cardenolide to cardanolide.
RF-3.2.2. Change "heteroatoms and groups" to "heteroatoms and characteristic groups".
RF-3.4. After 'Rule A-21.6' add '(ref 2) and R-1.3 (ref 3)'.
RF-3.5.2 (e). Correct second half of last sentence to "(see RF-10.1); if the two groups are identical and attached to an acyclic terminal double bond the group trans to the main chain is numbered first as described in the carotenoid recommendations Rule 12.4 (ref 5)."
RF-4.1.1 Note 1. Correct the carotenoid recommendation to 5.1.
RF-4.1.1 Note 2. Reword to "The use of 'nor' in norbornane to indicate the loss of three methyl groups is common but is discouraged. This usage should not be applied to any other monoterpenoid systems."
RF-4.1.1 last Note. Reword last sentence to "This system was recommended in the 2nd edition of the steroid rules [2S-7.1 (ref 9)] and is still used in Chemical Abstracts index nomenclature, but is not included in Section F because it is not as general as the locant system recommended here."
RF-4.1.2. Delete last sentence but retain "(e.g. Scheme 3)"
RF-4.2.2. Move this heading to after the note in RF-4.2.1.
RF-4.2.2.2. Correct the reference to 2S-7.4 (ref 9).
RF-4.3 example 3 (Scheme 11). Correct name to (16βH)-1,16-Cyclocorynan.
RF-4.4.1 Note and next paragraph. Change to "Note: The configurations at positions 15 and 20 of the secoyohimban in Scheme 12 are the same as those of yohimban. Reorientation of this portion of the molecule, as shown in Scheme 13, results in the hydrogen atoms at positions 15 and 20 apparently changing sides even though the configuration is unchanged. It is recommended that the configuration of substituents of such a seco-system is indicated by the R/S system."
RF-4.4.1 Example 2 (Scheme 12). Delete alternative name for 13,14-Secopodocarpane (inconsistent with RF-4.7.1)
RF-4.4.2 Note. Change to "This procedure is used only in carotenoid nomenclature (ref 5) (Scheme 15)."
RF-4.5.1 The prefix abeo should be described in terms of x(yz)-abeo-. Add the following note after the first paragraph.
"Note: Previously abeo was italicized (ref 1, 2, 3, 4). For consistency with the other modifying prefixes it is now recommended that a roman font be used. This change was not followed in the lignans and neolignans document (ref 8). The abeo nomenclature described in this recommendation is permissive, not compulsory. It is most suitable for use in discussions of reaction mechanisms and biogenesis. In general systematic names, or names assigned by the homo- and/or nor- method, are preferred."
RF-4.5.2. Change last sentence to "The prefix retro is used in this manner only in the nomenclature of carotenoids (ref 5) (e.g. Scheme 17)."
RF-4.5.2 example (Scheme 17). Correct structure of 4',11-retro-β,ψ-Carotene [both the 4'(5') and 6'(7') double bonds are E].
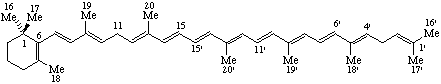
RF-4.7. Change the recommendations considered to "(RF-4.1 through RF-4.4, i.e. excluding bridges, fusion and detachable prefixes)."
RF-4.7.1. Change to "When different combinations of prefixes can be used to effect the same transformation in a parent structure, the combination of choice should express the fewest number of operations. Both detachable (e.g. alkyl) and non-detachable (e.g. homo or nor) prefixes are considered as modifications but detachable prefixes are preferred. Dihomo, dinor, etc., are counted as two modifications each [see Rule 3S-6.3 (ref 4)]. When the number of operations is the same, the combination of homo/nor is preferred to cyclo/seco; choice between other combinations expressing the same number of operations is based on earliest alphabetic order of the prefixes."
RF-4.7.1 example (Scheme 19). Change not name to: (9αH)-5,9-Cyclo-5,10-secoergoline. Another possible alternative name is (9αH)-5(109)-Abeoergoline.
RF-4.7.3 example 3 (Scheme 21). Change name to (2S,7αH,16αH)-7H-1,16:2,4-Dicyclo-3,4-secocorynan
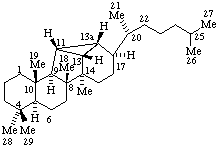
RF-4.7.3 example 4 (Scheme 21). Correct name to 9,19-Cyclo-4-nor-5α,9β-cholestane.
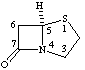
RF-4.7.3 example 6 (Scheme 22). Correct drawing and name to:
RF-4.7.4. Reword to "After satisfying RF-4.7.1 and RF-4.7.2, the prefixes that indicate bond rearrangements (cyclo, seco, etc.) are followed by those that indicate addition or removal of skeletal atoms (apo, homo, nor). If more than one of any of these operations is needed, they are cited in alphabetic order before the name of the parent structure. Schematically, this order is as follows:
| bond rearrangement | removal/addition of skeletal atoms | Parent structure |
| cyclo, seco | apo, homo, nor |
(Examples in Scheme 23)"
RF-4.7.4 Note. Reword to "This example can also be named (11βH)-7(811)-Abeo-17a-homo-5α-estrane which uses only two operations."
RF-4.7.4 (Scheme 24, top example). Delete Note and top example. (Inappropriate example where a systematic name is preferred.)
RF-4.7.4 example (Scheme 24, bottom example). Correct name to (17R,20S)-13,13a-Seco-13(17)a-homo-12-nordammarane
RF-5 Add reference R-2.3.3.2 (ref 3).
RF-5.2 example 1 (Scheme 26). Correct name to (4βH)-4-Carbayohimban.
RF-6.1. Add reference to RF-9.2.
RF-6.1 example 2 (Scheme 29). Correct name to Acetone 4,5α-epoxymorphinan-6β,7β-diyl ketal.
RF-6.2.1. Add reference to R-2.4.1.1 (3), FR-2.1 and FR-2.2 (7). Also change the last sentence to "Terminal vowels of the names of systematic components are not elided when followed by a vowel [this is consistent with the recommendation contained in the fused ring nomenclature report (ref 7) and is a change from previous recommendations (ref 2)]."
RF-6.2.1 examples 3 and 4 (Scheme 30). Correct name to 1H-[1,2]Oxazolo[4',3':17,18]yohimban and [1,2]Thiazolo[5',4',3':4,5,6]cholestane [isoxazole and isothiazole are no longer recommended (ref 7)].
Add after the text a new paragraph: "When two or more identical systematic components are fused to a natural product component primes are assigned to the systematic component attached to the lower numbered natural product positions, double primes to the next component, etc. (e.g. Scheme 30a). When there are two or more nonidentical systematic components these are cited in alphabetical order and primes are assigned in the same order (e.g. Scheme 30b)."
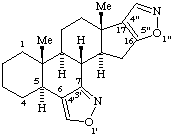
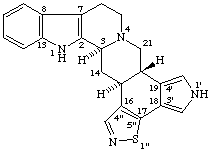
RF-6.2.2 Second and last sentence. Change to "If it is necessary to identify saturated positions on the systematic component (including the fusion sites) that have at least one hydrogen present, these are designated by the indicated hydrogen method [see A-21.6 (ref 2) and R-1.3 (ref 3)]. Unprimed locants are used to identify the position of the indicated hydrogen, where there is a choice (e.g, Scheme 32). For configuration at chirality centres which arise from the fusion process see RF-6.2.4." (new)
RF-6.2.2 (Scheme 31). Correct name to (8αH)-4,5α-Epoxy[1,3]oxazolo[5',4':8,14]morphinan.
RF-6.2.3 last sentence. Change to "Where there is a choice, the unprimed locants are used, (e.g. Scheme 33)."
RF-6.2.3 example 1 (Scheme 33). Change name to (6αH)-1',6-Dihydroazirino[2',3':5,6]-5β-androstane
RF-6.2.4. Reword: "The configuration at chirality centres which arise from the fusion process or their hydrogenated derivatives is indicated by the α/β system in accordance with its use in steroid nomenclature [see 3S-1.4, 3S-10.2 (ref 4) and RF-10], or, if necessary by the Sequence Rule method (R/S) (see also RF-10). The projection of the hydrogen atom below (α) or above (β) the reference plane of the ring system is indicated by the locant and the appropriate symbol, and a capital italic letter H, all cited within parentheses (examples in Schemes 31, 33, 34). Note that such a stereodescriptor does not replace indicated hydrogen (e.g. Schemes 34, 34a)."
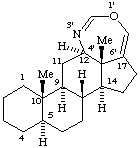
RF-6.2.4 example 2 (Scheme 34, example 1). Change name to (12αH,13βH,16βH,17αH)-3',4',5',6',12,13,14,15,16,17-Decahydrobenzo[16,17]erythrinan
RF-6.2.4 example 3 (Scheme 34, example 2). Change name to (20αH,21R)-20H-benzo[20,21]17(2221)-abeogammacerane (also has been named as a 1'H-Benzo[20,21]-A'-neogammacerane)
RF-7. example 4 (Scheme 35). Change alternative name to (16βH)-Thiireno[16,17]-5α-pregnane
RF-7. example 5 (Scheme 36). Change note to "(note that this name follows the published recommendations for carotenoids (ref 5), in which the bridge prefix 'epoxy' is treated as detachable, and unprimed locants precede primed locants for 'hydro')."
RF-8.1 Change first sentence to "Unsaturation in a compound whose parent structure (see RF-3 through RF-7) is fully saturated, or in the portion of a parent structure that is otherwise fully saturated, is indicated by changing -an to -ene, -adiene, -yne, etc.; -ane to -ene, -adiene, -yne, etc.; -anine to -enine, -adienine, -ynine, etc.; or -an- to -en-, -adien-, -yn-, etc. [see 3S-2.5 in the steroid nomenclature recommendations (ref 4), and Rule R-3.1.1 (ref 3)]."
RF-8.2 example 1 (Scheme 39). Change name to (3<&zi;,9αH)-2,3-Dihydro-5(109)-abeoergoline
RF-9. example 4 (Scheme 43). Change name to 1(14)a-Homoeburnamenin-1a-one
RF-9.2 example 2 (Scheme 44). Change name to Aspidospermidin-4-one ethylene dithioketal.
RF-9.3 example 3 (Scheme 45). Change name to (1R)-1-(17-Norcorynan-16-yl)-1,2,3,4-tetrahydroisoquinoline-6,7-diol (there is no defined orientation of isoquinoline so that the configuration must be specified by the R/S system).
RF-9.4 example 1 (Scheme 46). Correct name to (4ξ)-2,2,6'-Trimethyl-9',10'-didehydrospiro[1,3-dioxolane-4,8'-ergoline] (dehydro is a nondetachable prefix).
RF-10.1. penultimate sentence. Change to "In the case of a racemate, the enantiomeric structure drawn should be the one that shows the lowest numbered chiral center in the α configuration (see also RF-10.5)."
RF-10.2.1. Add to the text: "A change in configuration of a non-bridgehead side-chain that is part of the parent is denoted by the method specified for C-17 of steroids [see 3S-5.2 (ref 4)], where the α or β refers to the side-chain itself and not to the hydrogen atom at the same position."
RF-10.2.1. example 4 (Scheme 49, example 2). Change name to 13β-Abietane.
RF-10.2.1. example 6 (Scheme 49, last example). Correct name to (23R)-23-Hydroxy-14,15,16,17-tetradehydroveratraman-3β-yl β-D-glucopyranoside (dehydro nondetachable and Δ not double underlined).
RF-10.2.2 example 2 (Scheme 50). Correct name to (22S,25S)-5β,8α,16β,20β-Spirostan.
RF-10.3. Revise text to: "Configurational inversion at all chirality centers is indicated by the italicized prefix ent- (a contracted form of enantio-) placed in front of the complete name of the compound. This prefix denotes inversion at all chirality centres (including those due to named substituents) whether these are cited separately or are implied in the name (e.g. Scheme 53, 54)."
RF-10.3 example 2 (Scheme 53, second structure). Correct numbering for ent-Kaurane (C-18 and C-19 should be reversed).
RF-10.3 example 4 (Scheme 54, second structure). Correct name to:
RF-10.5. Change ent- to epi-.
Alkaloids Appendix. Aspidofractinine: add H at position 1.
Alkaloids Appendix. Daphnane: add αH missing from position 2.
Alkaloids Appendix. 18-Oxayohimban: add "18-" to name, otherwise ambiguous.
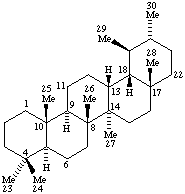
Steroids Appendix. Add new paragraph:
"The numbering of additional carbon atoms on a steroid sidechain was changed in the IUPAC-IUB Nomenclature of Steroids (Recommendations 1989). The older numbering is still used by Chemical Abstracts Service. The differences in the two numbering systems are shown in the following general formulae. As a consequence the numbering of campestane, ergostane, gorgostane, poriferastane and stigmastane was changed accordingly."
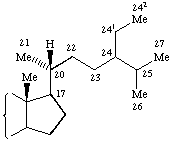 | 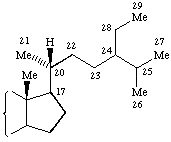 |
| IUPAC-IUBMB numbering | CAS numbering |
Steroids Appendix. Campestane: delete αH from position 5 (configuration not specified).
Terpenoids Appendix. Atisane: correct configuration at positions 5 and 9 (both αHs).
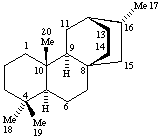
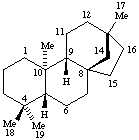
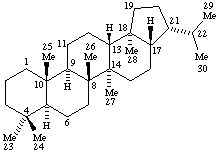
Terpenoids Appendix. Add Hopane.
Terpenoids Appendix. Add Thujane.
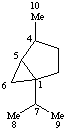
1. International Union of Pure and Applied Chemistry, "Nomenclature of Organic Chemistry. Section F: Natural Products and Related Compounds (Recommendations 1976)", IUPAC Information Bulletin, Appendices on Provisional Nomenclature, Symbols, Terminology, and Conventions, No. 53, December, 1976. (also in: Eur. J. Biochem. 86, 1-8 (1978) and [2]).
2. International Union of Pure and Applied Chemistry, Nomenclature of Organic Chemistry, Sections A, B, C, D, E, F and H, 1979 edition, Pergamon Press, Oxford, 1979.
3. International Union of Pure and Applied Chemistry, A Guide to IUPAC Nomenclature of Organic Compounds, Blackwell Scientific Publications, Oxford, 1993. Corrections Pure Appl. Chem., 71, 1327-1330 (1999).
4. International Union of Pure and Applied Chemistry and International Union of Biochemistry, Joint Commission on Biochemical Nomenclature, "Nomenclature of Steroids, Recommendations 1989", Pure Appl. Chem. 61, 1783-1822 (1989). [also in: Eur. J. Biochem. 186, 429-458 (1989) and pages xxx-lix in Dictionary of Steroids (Hill, R.A., Kirk, D.N., Makin, H.L.J. & Murphy, G.M., eds) Chapman & Hall, London 1991].
5. International Union of Pure and Applied Chemistry and International Union of Biochemistry, Commission on Biochemical Nomenclature, "Nomenclature of Carotenoids", Pure Appl. Chem., 41, 405-431 (1975).
7. International Union of Pure and Applied Chemistry, "Nomenclature of Fused and Bridged Fused Ring Systems (IUPAC Recommendations 1998)", Pure Appl. Chem., 70, 143-216 (1998).
8. International Union of Pure and Applied Chemistry, "Nomenclature of Lignans and Neolignans (IUPAC Recommendations 2000)", Pure Appl. Chem., 72, 1493-1523 (2000).
9. International Union of Pure and Applied Chemistry and International Union of Biochemistry, Commission on Biochemical Nomenclature, "The Nomenclature of Steroids Revised tentative rules, 1967.", Pure Appl. Chem., 31, 285-322 (1972). This 2nd edition has been superceded by the 1989 edition (ref 4).